Summary Concepts of Deep Learning

2016-03-01 Beijing

机器学习

input->feature representation->learning algorithm

监督学习

标注过的训练数据.

非监督学习

未标注的数据,让算法自己决定学到什么.

features

特征的表示对机器学习性能有巨大的影响.

神经网络

Neurons

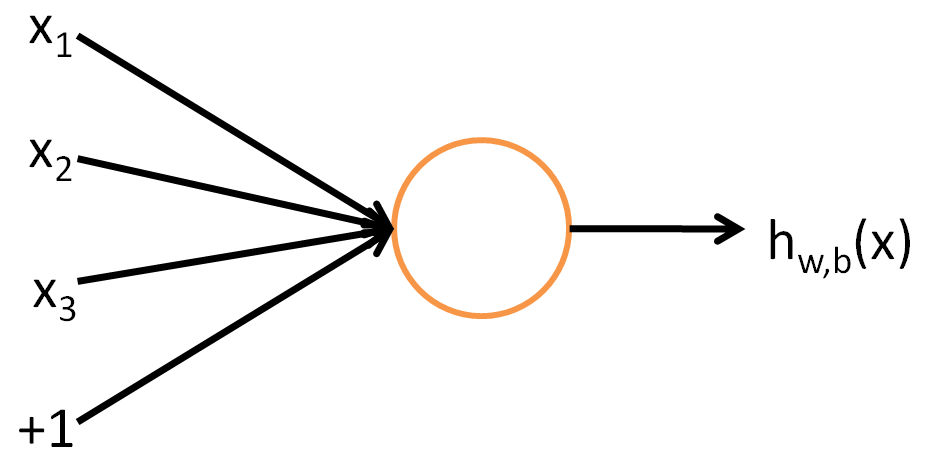
SingleNeuron

神经网络的基本组成单元,叫神经元(neuron),途中的神经元是一个以$x_1,x_x,x_3$(和一个$+1$截距项(intercept term))为输入,以$h_{W,b}(x)=f(W^Tx)=f(\sum_{i=1}^{3}(W_ix_i+b)$为输出的计算单元. 其中$f:\mathbb{R}\mapsto\mathbb{R}$,被称为激活函数(activation function).常用的激活函数有:

这些函数的形状如下:

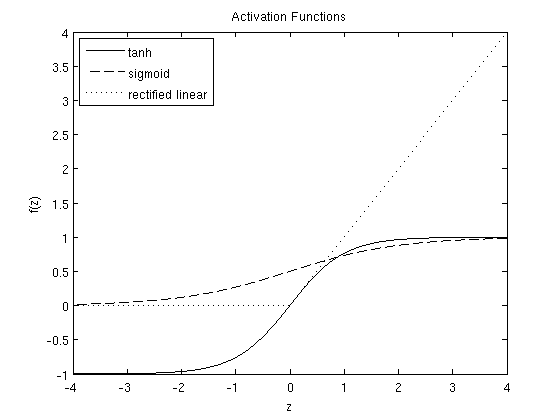
ActivationFunctions

神经网络模型

将一系列神经元组合在一起,就构成一个神经网络,一个神经元的输出可以作为另外一个神经元的输入.例如,下图是一个简单的神经网络:

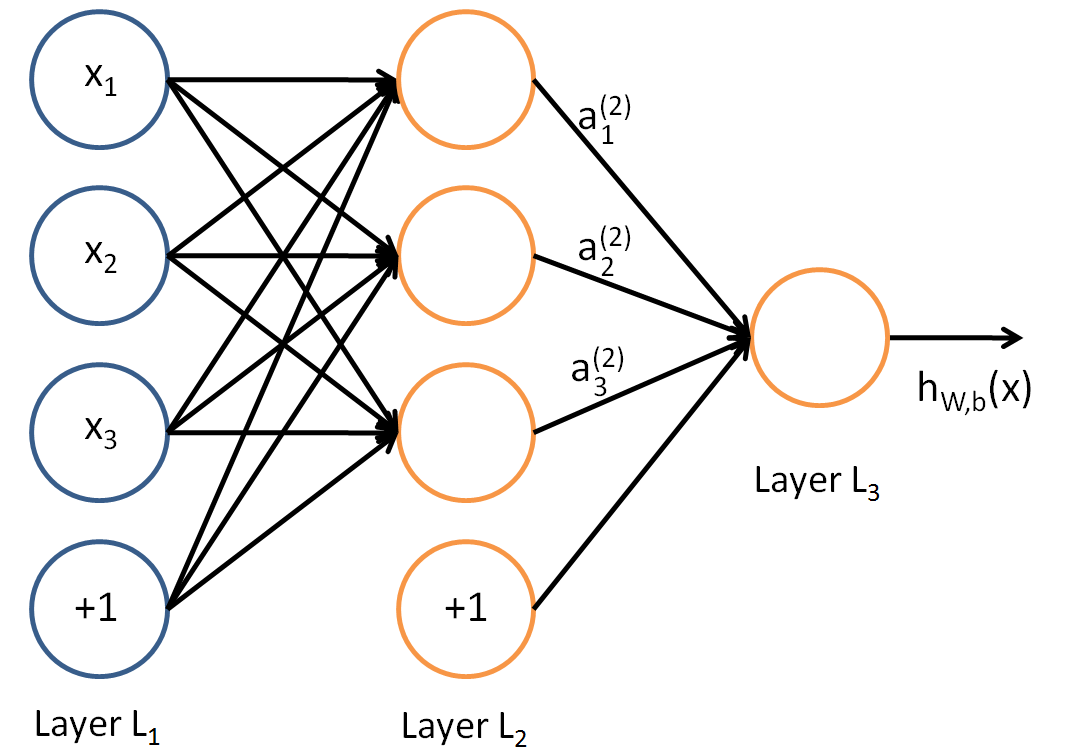
neualNetwork
在这个示意图中,黄色的圆圈代表神经元,蓝色的圆圈代表整个神经网络的输入.被标为$+1$的圆圈称作bias unit,代表截距项(intercept term). 网络最左边的层叫做输入层(input layer),最右边叫做输出层(output layer).中间所有的节点组成的层叫做隐藏层(hidden layer),因为我们不能在训练样本里面观察到它的值.

神经网络也可以有多个输出单元,比如,下面的神经网络有两个隐藏曾,$L_2$和$L_3$,输出层$L_4$有两个输出单元:

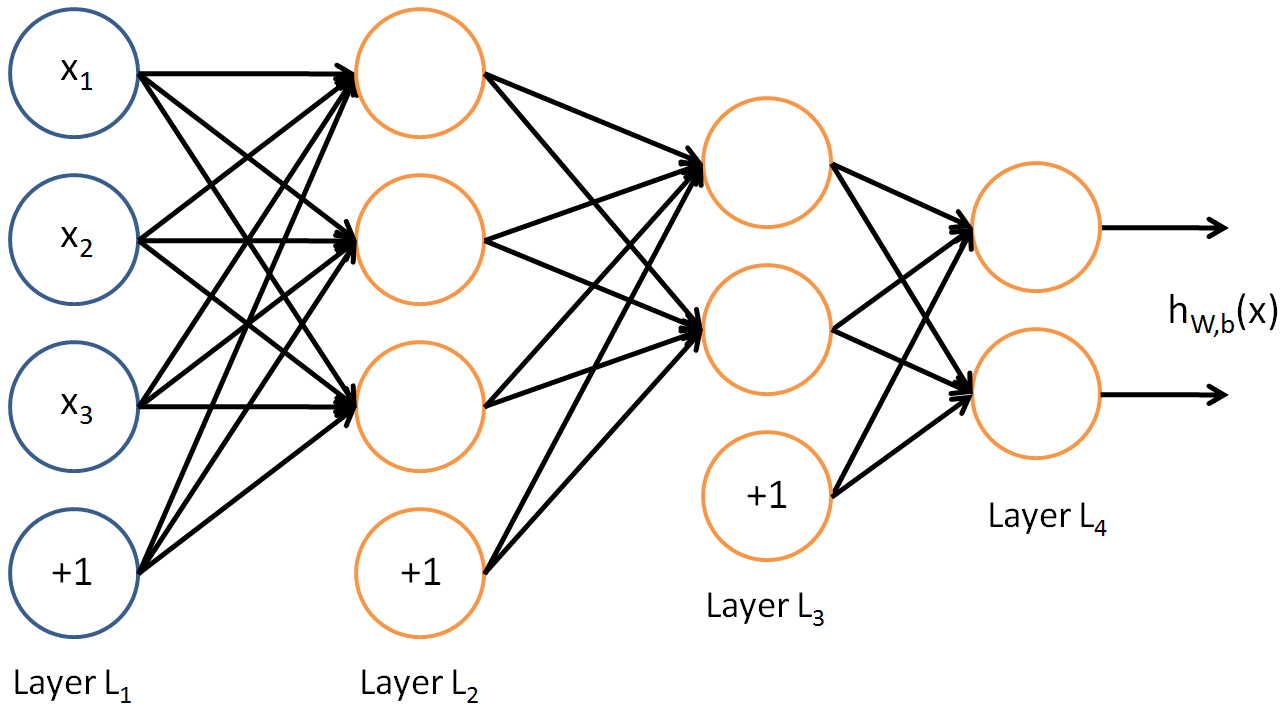
MultiOutputNetwork
如果你的任务是预测多个输出,这种神经网络很适用.

向前传播

每层每个节点的计算方法: $$ \begin{eqnarray*} a_1^{(2)} &=& f(W_{11}^{(1)}x_1 + W_{12}^{(1)} x_2 + W_{13}^{(1)} x_3 + b_1^{(1)}) \\ a_2^{(2)} &=& f(W_{21}^{(1)}x_1 + W_{22}^{(1)} x_2 + W_{23}^{(1)} x_3 + b_2^{(1)}) \\ a_3^{(2)} &=& f(W_{31}^{(1)}x_1 + W_{32}^{(1)} x_2 + W_{33}^{(1)} x_3 + b_3^{(1)}) \\ h_{W,b}(x) &=& a_1^{(3)} = f(W_{11}^{(2)}a_1^{(2)} + W_{12}^{(2)} a_2^{(2)} + W_{13}^{(2)} a_3^{(2)} + b_1^{(2)}) \end{eqnarray*} $$

我们用$z_i^{(l)}$ 表示第 $l$ 层第 $i$ 单元输入加权和（包括偏置单元），比如，$z_i^{(2)} = \sum_{j=1}^nW^{(1)}_{ij} x_j + b^{(1)}_i$,则 $a^{(l)}_i = f(z^{(l)}_i) $。 这样就可以得到一种更简洁的表示法。这里我们将激活函数 $ f(\cdot) $ 扩展为用向量（分量的形式）来表示，即 $ f([z_1, z_2, z_3]) = [f(z_1), f(z_2), f(z_3)]$ ，那么，上面的等式可以更简洁地表示为： $$ \begin{eqnarray*} z^{(2)} &=& W^{(1)} x + b^{(1)} \\ a^{(2)} &=& f(z^{(2)}) \\ z^{(3)} &=& W^{(2)} a^{(2)} + b^{(2)} \\ h_{W,b}(x) &=& a^{(3)} = f(z^{(3)}) \end{eqnarray*} $$ 我们将上面的计算步骤叫作前向传播。

向后传播

假设我们有一个固定样本集 ${ (x^{(1)}, y^{(1)}), \ldots, (x^{(m)}, y^{(m)}) }$，它包含$m$ 个样例。我们可以用批量梯度下降法来求解神经网络。具体来讲，对于单个样例 $(x,y)$，其代价函数为： $$ \begin{align} J(W,b; x,y) = \frac{1}{2} \left| h_{W,b}(x) - y \right|^2. \end{align} $$ 这是一个（二分之一的）方差代价函数。给定一个包含 $m$ 个样例的数据集，我们可以定义整体代价函数为：

$$ \begin{align} J(W,b) &= \left[ \frac{1}{m} \sum_{i=1}^m J(W,b;x^{(i)},y^{(i)}) \right] + \frac{\lambda}{2} \sum_{l=1}^{n_l-1} \; \sum_{i=1}^{s_l} \; \sum_{j=1}^{s_{l+1}} \left( W^{(l)}_{ji} \right)^2 \\ &= \left[ \frac{1}{m} \sum_{i=1}^m \left( \frac{1}{2} \left| h_{W,b}(x^{(i)}) - y^{(i)} \right|^2 \right) \right] + \frac{\lambda}{2} \sum_{l=1}^{n_l-1} \; \sum_{i=1}^{s_l} \; \sum_{j=1}^{s_{l+1}} \left( W^{(l)}_{ji} \right)^2 \end{align} $$

以上公式中的第一项 $J(W,b)$是一个均方差项。第二项是一个规则化项（也叫权重衰减项），其目的是减小权重的幅度，防止过度拟合。

我们的目标是针对参数 $W$和 $b$ 来求其函数 $J(W,b)$ 的最小值。为了求解神经网络，我们需要将每一个参数 $W^{(l)}_{ij}$ 和 $b^{(l)}_i$ 初始化为一个很小的、接近零的随机值（比如说，使用正态分布 $ {Normal}(0,\epsilon^2)$ 生成的随机值，其中 $\epsilon$ 设置为 $0.01$），之后对目标函数使用诸如批量梯度下降法的最优化算法。因为$J(W, b)$ 是一个非凸函数，梯度下降法很可能会收敛到局部最优解；但是在实际应用中，梯度下降法通常能得到令人满意的结果。最后，需要再次强调的是，要将参数进行随机初始化，而不是全部置为$0$。如果所有参数都用相同的值作为初始值，那么所有隐藏层单元最终会得到与输入值有关的、相同的函数（也就是说，对于所有$ i$，$W^{(1)}_{ij}$都会取相同的值，那么对于任何输入$x$ 都会有：$a^{(2)}_1 = a^{(2)}_2 = a^{(2)}_3 = \ldots ）$。随机初始化的目的是使对称失效。 梯度下降法中每一次迭代都按照如下公式对参数 $W$ 和$b$ 进行更新： $$ \begin{align} W_{ij}^{(l)} &= W_{ij}^{(l)} - \alpha \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b) \\ b_{i}^{(l)} &= b_{i}^{(l)} - \alpha \frac{\partial}{\partial b_{i}^{(l)}} J(W,b) \end{align} $$ 其中$\alpha$是学习速率。其中关键步骤是计算偏导数。我们现在来讲一下反向传播算法，它是计算偏导数的一种有效方法。

反向传播算法的思路如下：给定一个样例 $(x,y)$，我们首先进行“前向传导”运算，计算出网络中所有的激活值，包括$h_{W,b}(x)$ 的输出值。之后，针对第$l$ 层的每一个节点$i$，我们计算出其“残差”$\delta^{(l)}_i$，该残差表明了该节点对最终输出值的残差产生了多少影响。对于最终的输出节点，我们可以直接算出网络产生的激活值与实际值之间的差距，我们将这个差距定义为$\delta^{(n_l)}_i$ （第$ n_l$ 层表示输出层）。对于隐藏单元我们如何处理呢？我们将基于节点残差的加权平均值计算$\delta^{(l)}_i$，这些节点以$a^{(l)}_i$ 作为输入。下面是反向传导算法的细节

  1. 进行前馈传导计算，利用前向传导公式，得到 $ L_2, L_3, \ldots$ 直到输出层 $L_{n_l}$ 的激活值。

  2. 对于第$n_l$层（输出层）的每个输出单元$i$，我们根据以下公式计算残差： $$ \begin{align} \delta^{(n_l)}_i = \frac{\partial}{\partial z^{(n_l)}_i} \;\; \frac{1}{2} \left|y - h_{W,b}(x)\right|^2 = - (y_i - a^{(n_l)}_i) \cdot f'(z^{(n_l)}_i) \end{align} $$

  3. 对 $l = n_l-1, n_l-2, n_l-3, \ldots, 2$ 的各个层，第$l$ 层的第$i$个节点的残差计算方法如下： $$ \delta^{(l)}_i = \left( \sum_{j=1}^{s_{l+1}} W^{(l)}_{ji} \delta^{(l+1)}_j \right) f'(z^{(l)}_i)$$

  4. 计算我们需要的偏导数，计算方法如下: $$ \begin{align} \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x, y) &= a^{(l)}_j \delta_i^{(l+1)} \\ \frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x, y) &= \delta_i^{(l+1)} \end{align} $$

可以用矩阵-向量表示法重写以上算法。我们使用"$\bullet$" 表示向量乘积运算符。若 $a = b \bullet c$，则$a_i = b_ic_i$。反向传播算法可表示为以下几个步骤：

  1. 进行前馈传导计算，利用前向传导公式，得到$L_2, L_3, \ldots$直到输出层$L_{n_l}$ 的激活值。
  2. 对输出层（第$n_l$ 层），计算： $$ \begin{align} \delta^{(n_l)} = - (y - a^{(n_l)}) \bullet f'(z^{(n_l)}) \end{align} $$
  3. 对于 $l = n_l-1, n_l-2, n_l-3, \ldots, 2$ 的各层，计算: $$ \begin{align} \delta^{(l)} = \left((W^{(l)})^T \delta^{(l+1)}\right) \bullet f'(z^{(l)}) \end{align} $$
  4. 计算最终需要的偏导数值： $$ \begin{align} \nabla_{W^{(l)}} J(W,b;x,y) &= \delta^{(l+1)} (a^{(l)})^T, \\ \nabla_{b^{(l)}} J(W,b;x,y) &= \delta^{(l+1)}. \end{align} $$

批量梯度下降法中的一次迭代步骤如下:

  1. 对于所有$l$，令$\Delta W^{(l)} := 0$ ,$ \Delta b^{(l)} := 0$ （设置为全零矩阵或全零向量）
  2. 对于$i = 1 $到$m$，
    • 使用反向传播算法计算$\nabla_{W^{(l)}} J(W,b;x,y)$ 和$\nabla_{b^{(l)}} J(W,b;x,y)$。
    • 计算$\Delta W^{(l)} := \Delta W^{(l)} + \nabla_{W^{(l)}} J(W,b;x,y)$。
    • 计算$\Delta b^{(l)} := \Delta b^{(l)} + \nabla_{b^{(l)}} J(W,b;x,y)$。
  3. 更新权重参数： $$ \begin{align} W^{(l)} &= W^{(l)} - \alpha \left[ \left(\frac{1}{m} \Delta W^{(l)} \right) + \lambda W^{(l)}\right] \\ b^{(l)} &= b^{(l)} - \alpha \left[\frac{1}{m} \Delta b^{(l)}\right] \end{align} $$ 重复梯度下降法的迭代步骤来减小代价函数$J(W,b)$的值，进而求解神经网络。

神经网络的问题

Deep Learning

深度学习的基本思想

自编码器(Autoencoders)

假设我们只有一个没有带类别标签的训练样本集合 ${x^{(1)}, x^{(2)}, x^{(3)}, \ldots}$ ，其中$x^{(i)} \in \Re^{n}$ 。自编码神经网络是一种无监督学习算法，它使用了反向传播算法，并让目标值等于输入值，比如 $y^{(i)} = x^{(i)}$ 。下图是一个自编码神经网络的示例。

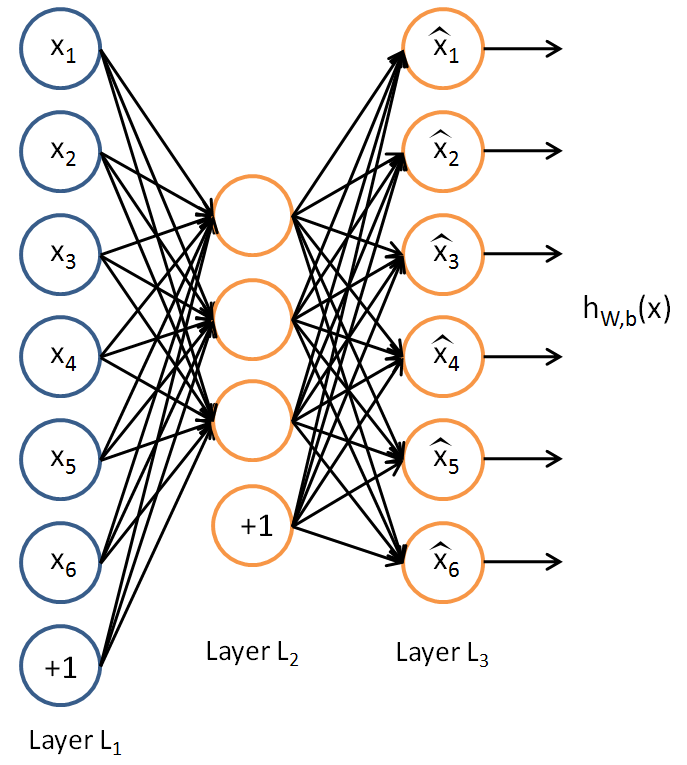
Autoencoder636
自编码神经网络尝试学习一个$ h_{W,b}(x) \approx x$ 的函数,它尝试逼近一个恒等函数，从而使得输出 $\hat{x}$ 接近于输入$x$.自编码神经网络的意义在于:

  1. 当我们限制隐藏神经元的数量让它小于输入的神经元个数,就可以得到输入的压缩表示(数据降维).
  2. 即使隐藏神经单元的个数比输入的神经元个数多,对自编码神经网络施加一些其他的限制条件也可以发现输入数据中的结构,比如,如果给隐藏神经元加入稀疏性限制，那么自编码神经网络即使在隐藏神经元数量较多的情况下仍然可以发现输入数据中一些有趣的结构。

在含有多个隐藏层的自编码神经网络中,每更高一层的隐层都是对低一层的更高阶的抽象.例如,当处理对象是图像时,可以用深度网络学习到"部分-整体"的关系.例如，第一层可以学习如何将图像中的像素组合在一起来检测边缘（正如我们在前面的练习中做的那样）。第二层可以将边缘组合起来检测更长的轮廓或者简单的“目标的部件”。在更深的层次上，可以将这些轮廓进一步组合起来以检测更为复杂的特征。

基本原理

深度学习的过程可以分为两步:

  1. 预训练:首先使用大量的未标注数据训练一个自编码器,这个自编码器能够从数据中学习到数据的最显著特征.
  2. 微调:再使用已标注数据对训练好的数据进行有监督学习(微调),从而得到最终想要的结果(这一步使用反向传播算法).

逐层训练方法

与神经网络使用反向训练的方法不同,神经网络使用逐层贪婪训练方法训练模型.主要思路是每次只训练网络中的一层，即我们首先训练一个只含一个隐藏层的网络，仅当这层网络训练结束之后才开始训练一个有两个隐藏层的网络，以此类推。在每一步中，把已经训练好的前$k-1$ 层固定，然后增加第$k$层（也就是将已经训练好的前$k-1$ 的输出作为输入）。每一层的训练可以是有监督的（例如，将每一步的分类误差作为目标函数），但更通常使用无监督方法(例如自动编码器).

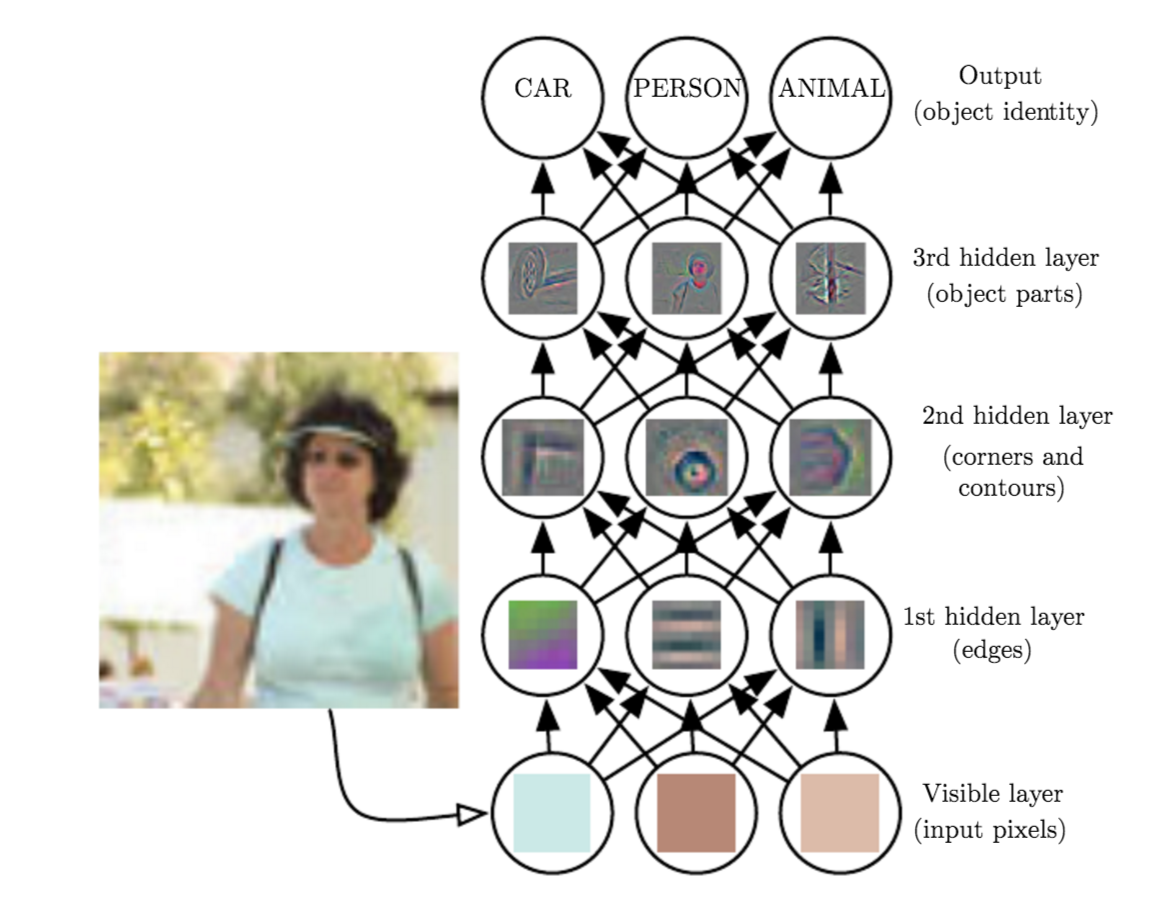
DeepLearningFeautures

深度学习的应用

  1. Deep Learning（深度学习）学习笔记整理系列 ↩

  2. Deep Learning ↩

  3. Deep Learning Tutorial ↩

  4. http://ufldl.stanford.edu/wiki/index.php/UFLDL%E6%95%99%E7%A8%8B ↩

© 2020 andy · Powered by Pelican, Hosted by Coding Pages